There’s some small growing pains on the welcome road to a more online government.
It’s not quite as amusing as when I get this kind of thing from Failblog, though.

Onion headline: “CIA Awkwardly Debriefs Obama On Creation Of Crack Cocaine”

                                       Packets               Pings
 Host                                Loss%   Snt   Last   Avg  Best  Wrst StDev
 1. 208.127.185.1                     0.0%   801    7.1   7.0   6.0  26.6   1.0
 2. LAX1.CR1.Gig6-0.dslextreme.com   64.1%   801   10.6   8.3   6.2  48.0   3.6

(The situation this morning from ~8 to ~11 o’clock.) TCP canna handle the strain, captain!

rsnapshot is a fantastically simple, easy-to-use application for performing backups of one computer to another. It uses rsync so that the data sent over the wire is encrypted and only that of an incremental backup. It uses hardlinks across snapshots for unchanged files, so you have full snapshots for all the backups kept, at only a fraction of the diskspace otherwise needed.

It has turned my remote backups from a pain to a simple matter of running a command every day or two and entering my password. Entering my password manually is the only deficiency I find with it. The rsnapshot docs recommend making a passphraseless ssh key for it to use, but I don’t trust that. Sometime I’ll have to look into if I can make a ssh key which’ll only allow rsnapshot to perform its rsync download, not log in or run other commands.

On Sunday I bought myself a new toy, an Asus Eee 900. The general opinion on the ’net seemed to be that the default Xandros Linux installed OS was inferior to Ubuntu Eee (note not a Canonical-endorsed project), so I installed it. I’m going to restrict my discussion to the software (you can find a lot written about Asus Eees themselves on the net).

The most serious problem by far is that WiFi was broken out of the box, due to faulty interaction of the wifi-on/-off and wifi-toggle ACPI event handlers. I found plenty of people complaining about this issue and several fixes by basic searching, but it’s utterly astounding to me that an OS distribution targeting a portable computer where WiFi is essential for its use could have this bug in release. The Eee exists to be a box accessing everything through wireless, no WiFi is a “game over, you lose”-level bug. It was also made more frustrating by the various networking tools not even showing wireless as an option unless it was already on. Better would be to show the wireless interface as there and down (as it was) and let the user select it to bring it up (which still wouldn’t have worked, but at least you’re not making them waste their time figuring out why it’s not there at all).

There were some issues that popped up earlier, even before the first boot in the install app. The select keyboard layout section has a text area where you can test typing, but it uses the current keyboard layout instead of the new one you’ve selected in the tool, uselessly. (The change keyboard layout tool once you’ve booted into the OS has the same problem.) The time of day shown when you’re selecting the local timezone is wrong (and it says you can set it to the right time after boot), though after booting it gets the time of day correct.

After getting wireless working, the update manager said updates were available, so I let it install them. It got halfway through, then the laptop suspended itself because it was idle. When I un-suspended it, WiFi and X didn’t come back up and asusosd was busying the CPU. Restarting X brought up a login window on virtual console 9 (only discovered by seeing X running on tty9 in ps), but I had to reboot to get WiFi back so the update could finish. (The Eee seems to resume fine when it’s genuinely idle at suspend.)

I copied the photos from my recent vacation onto its SSD, and went to view them in the file viewer you get from the “Pictures” folder. This brought up Eye of Gnome, and as my camera takes more pixels than the Eee’s display has, you have to scroll. Unfortunately, EOG doesn’t scroll when you make the normal scroll touchpad gestures, but instead changes zoom level. Also unfortunately, EOG doesn’t scroll when you press the arrow keys, but instead switches to other pictures in the CWD. So, to scroll in EOG it seems you have to move the mouse cursor to the arrows on the scrollbar and hold the mouse button down, which is a pretty crummy thing to ask of the user of an Eee. Also unfortunately, if you go to the help menu in the file viewer to try and learn how to change the preferred app for pictures to one which doesn’t suck as hard, you get an error dialog saying there’s no help. 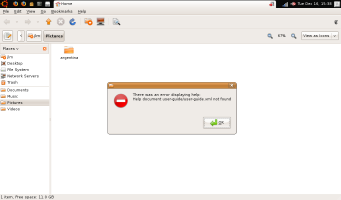Also also unfortunately, the “Preferred Applications” tool doesn’t let you change associations for pictures, only for a small handful of apps: Web browser, mail reader, terminal, and “multimedia” (videos & music) player.

Moving on to more minor stuff, at night, I turned the display brightness down, but twice it switched itself back up to full brightness a few seconds later. (Third time turning down seemed to stick, but it happened again this morning and took four turn-downs.) It was getting hot, because it wasn’t turning the fan on. (After installing cpufrequtils, the fan would turn on.) The Firefox start page is set to a file which isn’t installed. mtr needs root to run, and it’s not installed setuid.

The Eee’s “House” key does nothing — naturally, it should bring you back to the home menu display. This would be convenient, as you have to mouse over to the Ubuntu logo on the top left and click it to get there now, and the other top-left icons are available by cycling through Alt-Tab. There are often spurious mouse clicks generated by the touchpad when I’m trying to fine-position the mouse and it thinks I’ve tapped (the mouse should never require fine-positioning, but that seems to be a lost battle), and at the same time actual taps are often misinterpreted as short moves.

I’m not the first to run into these problems, they all seem to have been reported already, but that I’ve run into so many usability and functionality problems in so short a time means that Ubuntu Eee is clearly not ready for mainstream use. A sophisticated user can get around them (X didn’t come back after un-suspend? Alt-F1, login, start new X, ps, ah it’s on tty9, Alt-F9. — mtr can’t get raw socket? sudo chmod u+s =mtr) but it’s too much to expect from non-geeks, and falls well short of the goal of “it just works”. I’m optimistic about the future — hopefully Ubuntu Eee won’t make a release with such a severe bug ever again, and suspend/resume is getting a lot of work on it in the kernel right now, and a lot of this stuff just needs easy fixes (like putting the help files and start page where they’re looked for (Eye of Gnome OTOH has sucked for years and should just be taken out back and shot)). And it’s a pretty nice experience for me as a “power user”, once I’ve patched the wireless and gotten the big initial update complete and got my image viewer set to ImageMagick…, and I can accept the brightness resetting and suspend problems and the “House” key not working for a few more update cycles. But it’ll be a while still before the dreamed-of shiny usable Linux laptop arrives.

So, I’ve been pondering the market crash. (It seems like the only stuff on the news are it and the presidential campaign.) The mortgage failures which started it took down more than just the banks which unwisely made excessive subprime loans because these mortgages were bundled up and sold as securities, exposing other firms. Financial corporations then made derivative securities on them, instruments which would provide a payment if some fraction of the mortgage holders did (a “CDO”) or didn’t (a “CDS”) make their payments. They even took bunches of CDOs and made “secondary CDOs” from them.

The theory behind the secondary CDOs was that mortgages fail now and then, so the high-risk CDOs will fail now and then when they do. But, just by chance, a more-than-usual number of mortgage failures will cluster in one CDO and make it fail, while other seemingly identical CDOs continue to pay — sucks if you held the unlucky CDO. The secondary CDOs protect against the phenomenon of chance clustering, but as we saw, they’re completely vulnerable to coordinated failures. (The rating agencies foolishly assumed mortgage failures were mostly independent, but in fact they’re highly correlated with each other, and in the presence of correlation, secondary CDOs have more risk, because they also “protect” you from chance putting an atypical number of good mortgages in your pool, which saves some primary CDOs when the market-wide failure rate would have been enough to take them down.)

Everything came tumbling down because many firms were exposed to mortgage failures through these derivatives. But aren’t derivatives supposed to be good for markets? Because they let people buy and sell risk, they thicken the market by bringing in traders who want different risk profiles. If people start worrying, they can hedge; without derivatives, you can only sell off.

I think that derivatives did bolster the market here. But subprime mortgage instruments are a market that deserved to fail, and should have failed much sooner. Derivatives held the market up, spreading the risk wider and wider, until there was nobody left to underwrite hedges, and the collapse of the market pulled these exposed firms down with it. Without derivatives, the failure of the subprime market would have come sooner, and had less impact, taking down only the mortgage traders. It’s good to stabilize markets which shouldn’t fail. But some markets should fail, and spreading exposure to these markets far and wide is a bad thing indeed.

I set up IPv6 through 6to4, and found it to be surprisingly easy and simple — subject to the major proviso that you only want IPv6 on one box. This should be easy, 6to4 gives you every address from 2002:abc:123:0:0:0:0:0 to 2002:abc:123:ffff:ffff:ffff:ffff:ffff to play with. To get it on other boxes, you need to have the end of the 6to4 tunnel route IPv6 packets, and the end-hosts have to get IPv6 addresses from it. Which turns out to be a problem. It’s easy to give your router 2002:abc:123:0:0:0:0:0, but giving out IPv6 address doesn’t work — the client support for getting IPv6 addresses over DHCP is zilch. Easier to set up Teredo.

This is worrisome. Client vendors have been complaining that the ISPs aren’t deploying IPv6 routing and patting themselves on the back for having their systems support IPv6, without considering that it only works if manually set-up. Suppose some ISP did do all the work of making its network route IPv6 — their customers still aren’t going to be on the IPv6 net, because their computers never ask for IPv6 addresses over DHCP so the ISP never gives them any. Are we expecting each one to call customer support for their IPv6 address and how to tell it to their system? The Internet has as many users as it does because the software lets the computers be plugged together and figure out how to talk on their own, without the user having to know how any of that works. IPv6 can’t work until that’s the case for it as well. If reading an RFC ever enters the picture, you lose: 99.9% of the Internet’s users won’t bother. It has to be made so transparent that the end user needs to do nothing and won’t even notice that another routing protocol is processing the packets.

I’ll give you up only when the sun’s cold
And my hurting you is forbode
    Shan’t ever run aroun’
    Nor ever let you down
You’ve just been limerickrolled.

It’s the twenty-first century. Where are the flying cars? The videophones? What about the robot barbers and tailor engines? I’m kind of glad we didn’t get radium fireplaces though.

More images of the year 2000 from 1910 at the National Library of France.

gdb has this awesome feature that nobody seems to have heard of (including myself before today). You can set breakpoints by regex!

“help rbreak”